Software Search, Categories and Specials

Graphing Examples

A Scientific, Financial & Graphing Calculator for Windows

Dream Calculator Start

Graphing Sine & Cosine

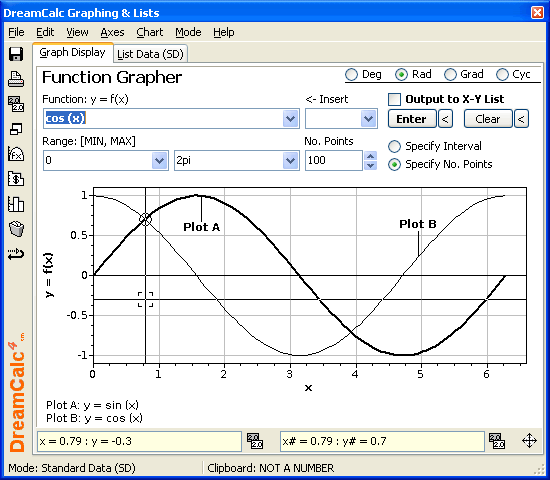
Sine & Cosine Functions

Input	Plot A: sin(x) Plot B: cos(x)
Range	0; 2pi
Angle Mode	Radians
No. Points	100
Notes

Square Wave with Random Noise

Input	SIGN(sin(x)) + 0.2 * Ran# - 0.1
Range	0; 3
Angle Mode	Cycles
No. Points	100
Notes	The SIGN function converts sine into a square wave, while Ran# adds "noise". The noise will change each time you plot the function.

Graphing an Asymptote

Asymptote

Input	1 / x
Range	-10; +10
Angle Mode	N/A
Interval	0.5
Notes	Use "Interval", not "No. Points" so as to create a discontinuity at x = 0 (i.e. 1 / 0 -> INFINITY).

Daylight Hours in London & New York

Total Daylight Hours in London (Plot A) & New York (Plot B) throughout the Year

Input	Plot A: x DLHRS 51.53 Plot B: x DLHRS 40.78
Range	1; 365
Angle Mode	Degrees
No. Points	100
Notes	The y-axis indicates the total hours of daylight throughout the year for London and New York. The x-axis is the day number. Plot A: London (latitude 51.53) Plot B: New York (latitude 40.78) DLHRS returns the number of daylight hours given a day-of-year and latitude, where: (doy) DLHRS (latitude). You can replace the latitude in the formula with your own. For more information about the DLHRS function.

Equation of Time

Input	9.87 * sin (2 * 360 * (x - 81) / 364) - 7.53 * cos (360 * (x - 81) / 364) - 1.5 * sin (360 * (x - 81) / 364)
Range	1; 365
Angle Mode	Degrees
No. Points	100
Notes	The "equation of time" approximates the difference between the apparent time and mean time (i.e. between solar noon and noon on the clock) throughout the year. The difference is due to a combination of the obliquity of the Earth's rotation axis and the eccentricity of its orbit.

Creating a Polar Chart

Polar Chart

Input	exp(cos(x)) - 2 * cos(4*x) + sin(x/12)
Range	1; 12pi
Angle Mode	Radians
No. Points	2000
Notes	Enter the above equation and select: Axes->Polar Plot.

Histogram Chart

Histogram Chart in Standard Data Mode

Mode	Standard Data (SD)
Chart	Histogram (Auto)
Data (Val, Fq)	(5, 1) (15, 3) (25, 8) (35, 18) (45, 24) (55, 22) (65, 15) (75, 8) (85, 0) (95, 1)

Cashflow Chart

Cashflow Chart (Professional Edition Only)

Mode	Any - cashflows are independent.
Chart	Cashflow
Cashflow	-2000, 3232, 7000, 9535, 13500, 21543, 12545, 18232, 11033, 7543, 5075

Quadratic Function Plot & X-Y Regression

This is an exercise where we will use the Function Grapher to generate a quadratic equation plot and export the data points to the X-Y list. We will then plot the X-Y list points with a quadratic line of best fit and determine the coefficient values used to originally create the graph.

1. To begin, put the calculator into Quadratic X-Y mode, i.e. select: Mode->Quadratic Regression Mode.
2. Go to the Function Grapher, i.e. Chart->Function Grapher.
3. Important: Check the Output to X-Y List box.

Quadratic Plot with Minimal Three Points

Input	1.2x^2 - 3x + 5
Range	-2; +4
Angle Mode	N/A
No. Points	3
Notes	We have chosen only 3 points because that is the minimum needed for quadratic regression, but you may use more if you wish.

5. Switch from the Function Grapher to an X-Y plot, i.e. select: Chart->Scatter Points.
6. Ensure that the Chart->Show Regression Fit menu option is checked.

Quadratic Regression Plot

If the information at the bottom of chart is not visible, select: View->Show Footer.

Here we can that see our original quadratic equation has been determined from the points in the X-Y list, as described by the coefficients values: +1.2, -3, +5 respectively.

Dream Calculator Start | Graphing a Function

Special! Free Choice of Complete Excel Training Course OR Excel Add-ins Collection on all purchases totaling over $70.00.
ALL purchases totaling over $150.00 gets you BOTH! Purchase MUST be made via this site. Send payment proof to [email protected] 31 days after purchase date.

Download Demo | Developers Site | Dream Calculator Standard Safe & Secure Payment Options

Pricing:

1	$25.99 USD
2 - 4 Licenses	$23.99 USD
5 - 9 Licenses	$22.99 USD
10+ Licenses	$19.99 USD

Compare Versions

Download Demo | Developers Site | Dream Calculator Professional Safe & Secure Payment Options